Vzpěrná únosnost členěných průřezů
Vzpěrná únosnost při vybočení kolmo ke hmotné ose je dána vztahem
kde je: | χ |
|
A |
| |
fy |
| |
γM1 |
|
Pro průřezy 4. třídy se počítá s efektivní plochou průřezu Aeff.
Pro vybočení kolmo ke hmotné ose y je štíhlost λy dána vztahem
kde je: | Lcr,y |
|
iy |
|
Poměrná štíhlost 
je dána vztahem
kde je: | λy |
|
λ1 |
| |
Aeff |
| |
A |
|
Hodnota štíhlosti λ1 pro výpočet poměrné štíhlosti je spočtena vztahem
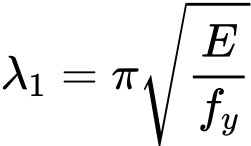
kde je: | E |
|
fy |
|
Pro hodnotu 
a tvar posuzovaného průřezu je stanovena hodnota součinitele imperfekce α, která reprezentuje jednu ze čtyř křivek vzpěrné pevnosti a, b, c, d. Součinitel vzpěrnosti χy je pak počítán ze vztahu
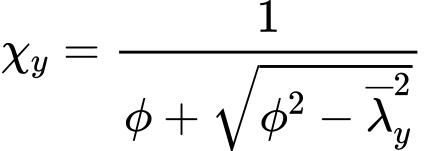
avšak musí být splněno, že
kde φ je získáno dle následujících vzorců
Pokud je zadaná osová síla v průřezu větší než únosnost Nb,Rd,y, průřez nevyhovuje a výpočet končí.
Dále se posuzuje vzpěrná únosnost při vybočení kolmo k nehmotné ose. Je vypočtena kritická síla Ncr podle vztahu
kde je: | lcr,z |
|
E |
| |
Ieff |
|
Pro příhradové spojky je Ieff počítán ze vztahu
kde je: | A |
|
h0 |
|
Pro rámové spojky se nejdřív spočte moment setrvačnosti průřezu I1 podle vztahu
kde je: | A |
|
h0 |
| |
Iz |
|
Pak se spočítá poloměr setrvačnosti průřezu i0
Pro hodnotu štíhlosti danou vztahem
se přiřadí hodnota součinitele μ a moment setrvačnosti Ieff se spočte podle vztahu
Pokud je zadaná osová síla větší než kritická síla Ncr, průřez nevyhovuje a výpočet končí.
Dalším krokem je výpočet smykové tuhosti SV. Pro rámové spojky je smyková tuhost dána vztahy
případně
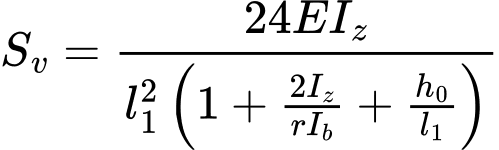
ale musí být splněno že
kde je: | l1 |
|
r |
| |
Ib |
| |
h0 |
|
Je-li zadaná osová síla větší než smyková tuhost SV, průřez nevyhovuje a výpočet končí. Je-li dále
průřez rovněž nevyhovuje a výpočet končí.
Síla v dílčím prutu uprostřed délky mezi spojkami je pro rámové spojky dána vztahem
pro spojky příhradové pak vztahem
v nichž moment MS je určen vztahem
kde je: | e0 |
|
Vzpěrná únosnost prutu je dána vztahem
kde je: | χz |
|
A |
| |
fy |
| |
γM1 |
|
kde součinitel vzpěrnosti χz je určen pomocí štíhlosti λ dané vztahem
kde je: | l1 |
|
imin |
|
Poměrná štíhlost 
je dána vztahem
kde
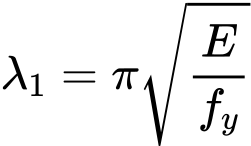
Pro hodnotu 
a tvar posuzovaného průřezu je stanovena hodnota součinitele imperfekce α, která reprezentuje jednu ze čtyř křivek vzpěrné pevnosti a, b, c, d. Součinitel vzpěrnosti χz je pak počítán ze vztahu
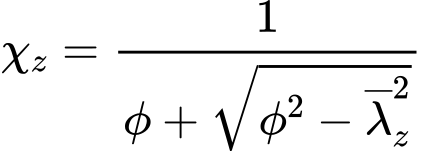
avšak musí být splněno, že
kde
kde
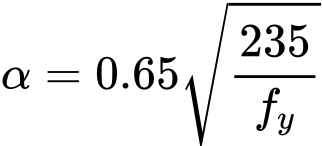
V místě spojky se vypočítává smyková síla VS
a moment Mz,Sd působící na dílčím průřezu vlivem spojek
kde je: | l1 |
|
Vy |
|
Únosnost dílčího prutu na ohyb od momentu My je dána pro průřezy 1. a 2.třídy vztahem
, pro průřezy 3.třídy vztahem
a pro průřezy 4.třídy vztahem
kde je: | Wpl,y |
|
Wy |
| |
Wy,eff |
|
Únosnost dílčího prutu na ohyb od momentu Mz se pak vypočte pro průřezy 1. a 2.třídy vztahem
, pro průřezy 3.třídy vztahem
a pro průřezy 4.třídy vztahem
kde je: | Wpl,z |
|
Wz |
| |
Wz,eff |
|
Posouzení se nakonec provádí ve dvou řezech. Uprostřed délky dílčího prutu a v místě spojky.
Uprostřed délky dílčího prutu se využívá podmínky
kde je: | n |
|
dN |
| |
ky |
|
V místě spojky má podmínka tvar
