Edometrický modul
Pokud naměřené veličiny z edometrické zkoušky vyjádříme edometrickou křivkou (v závislosti Δε = f(Δσef)), vidíme, že pro každý bod křivky dostáváme jiný poměr σef /ε.
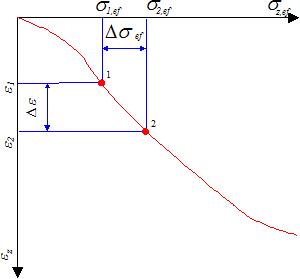 Určení edometrického modulu přetvárnosti Eoed
Určení edometrického modulu přetvárnosti Eoed
Pokud nahradíme deformační křivku pro určitý interval blízkých napětí σ1ef - σ2ef sečnou, můžeme závislost považovat za lineární a stlačitelnost zeminy určit poměrem Δσef/Δε - nazývaným edometrickým modulem přetvárnosti. Edometrický modul přetvárnosti Eoed je tedy sečnový modul, platný pro určitý interval napětí σ1ef - σ2ef na deformační křivce Δε = (Δσef):
![]()
Edometrický modul přetvárnosti Eoed má obecnou tendenci zvyšovat svoji hodnotu s rostoucím rozsahem napětí. Proto by měl být v každé vrstvě uvažován pro výpočet sedání edometrický modul přetvárnosti Eoed odpovídající příslušnému rozsahu napětí původního a konečného - tj. měl by být v každé vrstvě jiný. Této skutečnosti odpovídá i možnost zadávání edometrického modulu zeminy Eoed v programu, kdy je možné zadat pro každou zeminu edometrickou křivku (závislost σef/ε).
Z praxe je však známé, že např. u jílů je rozdíl Eoed určeného přepočtem z modulu přetvárnosti Edef a zjištěného zatěžovací zkouškou v terénu až několikanásobný.
Převod mezi modulem deformace Edef a modulem edometrickým Eoed je dán podle následujícícho vztahu:
![]()
![]()
kde: | ν | - | Poissonovo číslo |
Edef | - | modul přetvárnosti |
Orientační rozmezí edometrického modulu přetvárnosti Eoed pro jednotlivé zeminy v rozsahu napětí vyskytujícím se nejběžněji při zakládání staveb (prof. I. Vaníček: Mechanika zemin):
Zemina | Modul přetvárnosti Eoed [MPa] |
štěrkovitá | 60 - 600 |
písčitá středně ulehlá až ulehlá | 7 - 130 |
soudržná | 2 - 30 |
Literatura:
Vaníček, I.: Geomechanika 10: mechanika zemin. 3. přepracované vydání, Praha, ČVUT, 2000, 229 s., ISBN 80-01-01437-1.