在线帮助

Primární sedání

Konečné primární sedání s se často nahrazuje pojmem sedání. Většina základních výpočetních postupů se dá podle přístupu k řešení rozdělit do dvou skupin:- lineární pružná deformace- nelineární pružná deformace.

Lineární pružná deformace

Lineární závislost mezi napětím a přetvořením je popsána Hookovým zákonem:

Použití Youngova modulu E (často nazývaného modul pružnosti) je platné pouze pro případ, kdy je zatížené zemině umožněno roztažení ve směru vodorovném, což ve skutečnosti platí jen pro malé základové patky. Při zatížení větší plochy se mimo jejích okrajů nemůže zemina deformovat do stran a je tedy zatížena jednoosou deformací, která je popsána edometrickým modulem přetvárnosti E_oed, který je větší než modul pružnosti E.

Sedání vrstvy zeminy s je určeno přenásobením přetvoření vrstvy zeminy ε její mocností (výškou) H_o:

V případě vrstevnatého podloží je sedání rovno součtu deformací jednotlivých vrstev:

Nelineární pružná deformace

U většiny zemin je závislost mezi napětím a přetvořením nelineární, navíc často ovlivněna historií zatížení zeminy. Tato nelinearita se při výpočtu sedání jemnozrnných zemin (siltů, jílů) nemůže zanedbat. Je tedy zcela patrné, že výpočet sedání pomocí modulu pružnosti nelze použít obecně. I když budeme aplikovat výpočet pomocí edometrického modulu přetvárnosti vyjádřeného v závislosti na napětí v zemině, nepostihneme plně chování některých překonsolidovaných zemin. Nelineární pružná deformace je obecně modelována pomocí změny čísla pórovitosti a deformačních charakteristik zjištěných při jednoosé deformaci zeminy (tj. např. součinitel stlačitelnosti, index stlačitelnosti apod.).

Výpočet přetvoření stlačitelné vrstvy nenasycené zeminy pomocí čísla pórovitosti e si popíšeme na prvku této zeminy, který má výšku H_o a šířku B = 1 m:

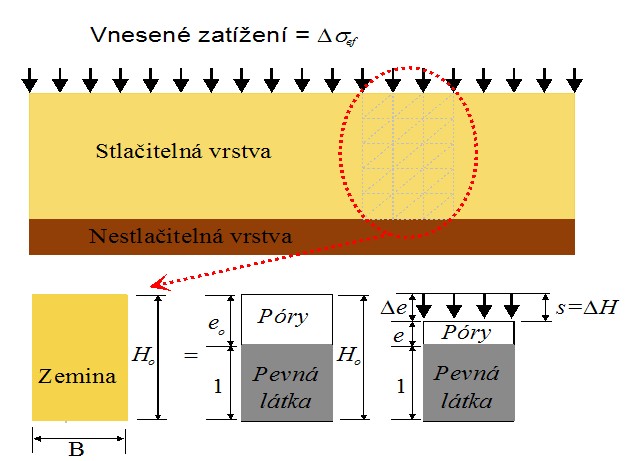Výpočet sedání z fázového diagramu

Vzhledem k tomu, že zemina je trojfázový materiál (obsahuje látky pevného, kapalného i plynného skupenství), můžeme pevné částice zeminy (skelet, tj. úlomky hornin a zrna minerálů) popsat jejich objemem V_s (a považovat jej za jednotkový) a póry zeminy popsat pomocí čísla pórovitosti e.

Vyjmutý prvek zeminy přitížíme na horním povrchu svisle rovnoměrným zatížením q, tím vyvoláme změnu napětí ve vzorku zeminy a následně jeho svislou deformaci ΔH, která má za následek zmenšení objemu pórů V_p a tedy i čísla pórovitosti (z počátečního čísla e_o na číslo e). Svislé relativní stlačení (přetvoření) prvku zeminy ε je dané poměrem svislé deformace ΔH prvku a jeho původní výšky H_o, a je možné jej vyjádřit pomocí čísla pórovitosti e:

Úpravou této rovnice dostaneme vztah pro sedání vzorku pomocí změny čísla pórovitosti: