Stufenartige Gleitfläche
Wenn der Gesteinsmassiv ein System von parallelen diskontinuierlichen Rissen aufweist, die zur Vorderseite der Felswand geneigt sind und das zweite System undeutlich ist, ist es möglich, die Bildung der stufenartigen (gezahnten) Gleitfläche im Gesteinsmassiv betrachten. Der Einfluss dieser Fläche kann durch der Calla- und Nicholas-Theorie in das Programm eingeführt werden, wodurch der Scherwiderstand an der stufenartigen Gleitfläche um Δτ erhöht wird.
![]()
![]()
wo: | σn | - | Normalspannung, die senkrecht zur Scherfläche wirkt |
ν | - | Welligkeitswinkel | |
T | - | effektive Zugfestigkeit von Stufen aus intaktem Gestein | |
k | - | Teil der Höhe ht, die den Stufen im intakten Gestein zugeordnet ist (nicht durch den sekundären Flächensystem entstanden wird) | |
ht | - | Senkrechthöhe des stufenartigen Keils, der auf der Neigung des Hauptsystems der Diskontinuitätsflächen liegt | |
T0 | - |
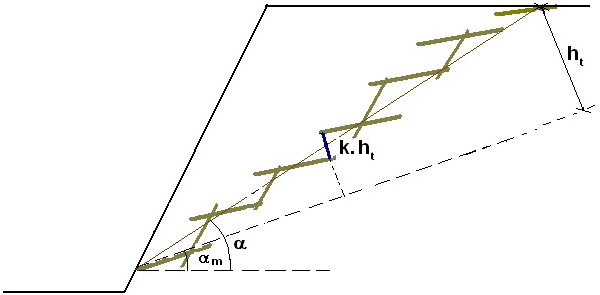 Stufenartige Gleitfläche
Stufenartige Gleitfläche
Literatur:
W.S. Dershowitz, H.H. Einstein - Characterizing rock joint geometry with joint system models Journal Rock Mechanics and Rock Engineering, Springer Wien ISSN 0723-2632 , Issue Volume 21, Number 1 / January, 1988 Pages 21-51.