Softening and Hardening
Standard formulation of the Drucker-Prager and Modified Mohr-Coulomb models assumes elastic rigid-plastic behavior of the soil, when the strength parameters of soil c and φ remain constant during the analysis. The enhanced version of both models ("Advanced program options" on) allows for the evolution of these parameters as a function of the equivalent deviatoric plastic strain:
![]()
![]()
where: |
| - | equivalent deviatoric plastic strain is given by the following expressions: |
![]()
![]()
![]()
where: |
| - | equivalent deviatoric plastic strain |
| - | deviatoric plastic strain tensor | |
| - | plastic strain tensor | |
| - | volumetric plastic strain | |
| - | Kronecker’s delta |
The assumed, piecewise linear, variation of strength parameters is evident from figure.
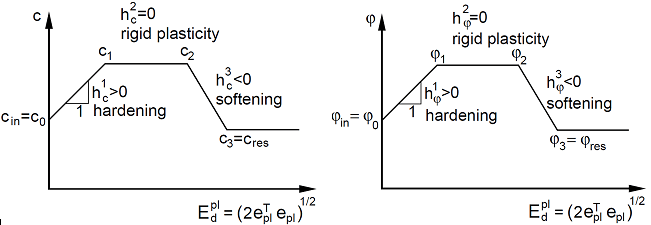 Multi-linear hardening-softening law: dependence of a) cohesion and b) angle of internal frintion on equivalent deviatoric plastic deformation Edpl
Multi-linear hardening-softening law: dependence of a) cohesion and b) angle of internal frintion on equivalent deviatoric plastic deformation Edpl
Dilation angle ψ can be assumed either constant or it may evolve as a function of the angle of internal friction φ following the Rowes dilation theory:
![]()
where φcv is the angle of internal friction at constant volume consistent with the critical state of soil (state at which the soil deforms at zero volumetric plastic strains). To prevent an infinite increase of the dilation angle (increase of tensile volumetric plastic strains) it must be bounded, e.g. in dependence on the maximum void ratio emax, acceptable for a given material. The Rowes dilation theory requires the introduction of the following parameters:
φcv | - | angle of internal friction at constant volume [-] |
e0 | - | initial void ratio |
emax | - | maximum void ratio [-] |
The current void ratio e can be expressed in terms of the current volumetric strain εv and the value of initial void ratio e0 as:
![]()
![]()
where: | e | - | current void ratio |
e0 | - | initial void ratio | |
εv | - | overall volumetric strain |
When the current void ratio e exceeds the maximum void ratio emax, the dilation angle ψ is set to 0.