EN 1995-1-1 (EC5)
Vérification de la flexion et de la compression
La résistance à la flexion de calcul du bois est donnée par :
![]()
où : | fm, k | - | résistance à la flexion caractéristique du bois |
kmod | - | coefficient de l'effet de charge et d'humidité | |
γM | - | coefficient partiel des propriétés du bois |
La résistance à la compression de calcul du bois est donnée par :
![]()
où : | fc, k | - | résistance à la compression caractéristique du bois |
kmod | - | coefficient de l'effet de charge et d'humidité | |
γM | - | coefficient partiel des propriétés du bois |
Le critère d’admissibilité est défini par :
![]()
où : | σc,0,d | - | contrainte en compression de calcul |
σm,d | - | contrainte en flexion de calcul |
et le taux de travail par :
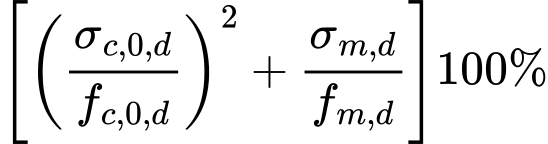
Vérification de la flexion et de la traction
La relation suivante définit la résistance à la traction de calcul du bois :
![]()
où : | ft, k | - | résistance à la traction caratéristique du bois |
kmod | - | coefficient de l'effet de charge et d'humidité | |
γM | - | coefficient partiel des propriétés du bois |
Le critère d’admissibilité est défini par :
![]()
où : | σt,0,d | - | contrainte de traction de calcul |
σm,d | - | contrainte de flexion de calcul |
et le taux de travail par :
![]()
Vérification du cisaillement
La résistance au cisaillement de calcul du bois est donnée par :
![]()
où : | fv, k | - | résistance au cisaillement caractéristique du bois |
kmod | - | coefficient de l'effet de charge et d'humidité | |
γM | - | coefficient partiel des propriétés du bois |
L'inégalité suivante définit le critère d’admissibilité :
![]()
où : | τd | - | contrainte de cisaillement de calcul |
kcr | - | coefficient de la largeur de section en glissement |
et le taux de travail est fourni par :
![]()