Module sécant du sol Es
La littérature spécialisée fournit deux définitions du module du sol Es. Selon Poulos et Davis (1980) ce paramètre fait référence au module élastique du sol (module de Young), tandis que Briaud (2001) et Gopal Ranjan (2000) nomment ce paramètre module sécant du sol. Ces deux définitions ont pratiquement le même sens. Cependant, le sol ne se comporte de manière élastique que dans le domaine des petites déformations (il s’agit généralement d’un matériau hétérogène); il est donc plus approprié de parler du module sécant du sol Es.
La courbe déviateur-déformation axiale permet de déterminer le module d'élasticité du sol E. Le module non drainé Eu provient des résultats de tests triaxiaux non drainés, le module drainé Ed de tests en conditions drainées.
Au début de la courbe de déformation, la dépendance est presque linéaire, mais la déformation élastique du sol est très faible par rapport à la valeur totale de la déformation. Ainsi, on distingue le module tangent, le module sécant et le module tangent initial. L'introduction de cette hypothèse simplificatrice permet d'utiliser la théorie de l'élasticité pour détecter l'état de contrainte-déformation dans les sols.
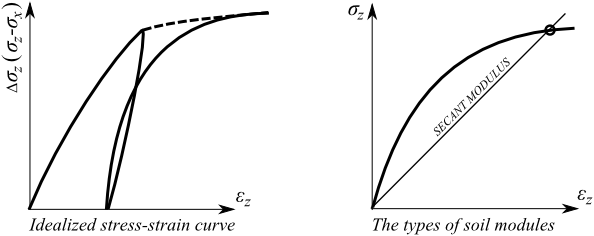 Courbe contrainte-déformation idéale et détermination des types de modules de sol
Courbe contrainte-déformation idéale et détermination des types de modules de sol
Le module de déformation sécant du sol Es est défini comme le rapport de la différence de déviateur de contrainte normale à la déformation axiale correspondante du sol (ou de façon équivalente la pente d'une droite tracée de l'origine de la courbe contrainte-déformation d'un matériau à un point de la courbe correspondant à une contrainte donnée), la relation suivante permet de le calculer :
![]()
Lambe et Whitman (1969) indiquent que le module d'élasticité d'un sol est généralement le module sécant allant d'un déviateur de contrainte normale nul à un déviateur de contrainte égal à la moitié (ou au tiers) du déviateur de contrainte maximal.
Le module sécant Es diminue lorsque le niveau de contrainte augmente, car la courbe contrainte-déformation a une courbure descendante. Il existe trois moyens d'obtenir ce paramètre :
- essais triaxiaux en laboratoire (calcul basé sur le module tangent du sol)
- test de charge statique de pieux
- relations de corrélation empiriques basées sur l'expérience passée.
Valeurs caractéristiques du module de déformation sécant Es pour des sols donnés - valeurs obtenues lors d'essais in situ en fonction de l'historique des contraintes, de la teneur en eau, de la consistance ou de la densité du sol (Gopal Ranjan et Rao, 2000) :
Type de sol | Consistance ou densité du sol | Module Es [MPa] |
Limon argileux | Très mou | 0,2 - 2 |
Argile | Très molle | 2 - 15 |
Molle | 5 - 25 | |
Ferme, moyenne | 15 - 50 | |
Résistante, dure | 50 - 100 | |
Sableuse | 25 - 250 | |
Limon sableux | Limoneux | 7 - 21 |
Léger | 10 - 24 | |
Dense | 48 - 80 | |
Sable et gravier | Léger | 50 - 145 |
Dense | 100 - 190 |
Littérature :
Briaud, J.-L.: Introduction to Soil Moduli. Geotechnical News, June 2001, BiTech Publishers Ltd, Richmond, B.C., Canada.
Gopal Ranjan et. A. S. R. Rao: Basic and Applied Soil Mechanics. New Age International, 2000, chapter 10.11, pp. 328 - 330. ISBN: 8122412238, 9788122412239.
Lambe, T. W. et. Whitman, V. R.: Soil Mechanics. New York: John Wiley and Sons, 1969, 576 p. ISBN: 978-0-471-51192-2.
Poulos, H. G. et. Davis, E. H.: Pile Foundations Analysis and Design. New York: John Wiley and Sons, 1980, chapter 5.5, pp. 101 - 104.