在线帮助

Sarma

La méthode de Sarma s'inscrit dans une catégorie de méthodes des tranches générales des états limites. Elle est basée sur la satisfaction des conditions d'équilibre des forces et des moments sur des blocs individuels. Les blocs sont créés en divisant la région du sol au-dessus de la surface de glissement potentielle par des plans qui peuvent généralement avoir des inclinaisons différentes. Les forces agissant sur les blocs individuels sont représentées sur la figure suivante.

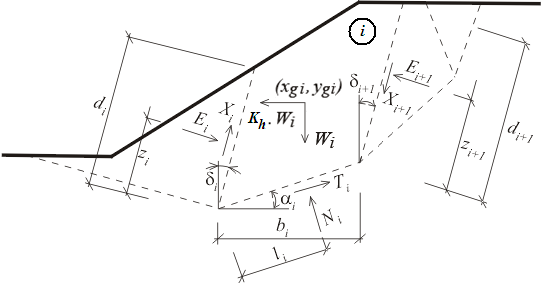Schéma statique - méthode de Sarma

Ici E_i , X_i représentent les forces normales et de cisaillement entre les blocs. N_i , T_i sont les forces normales et de cisaillement sur les segments de la surface de glissement. W_i est le poids du bloc et K_h*W_i est la force horizontale utilisée par la méthode de Sarma pour terminer l'état limite. Généralement une surcharge inclinée peut être introduite dans chaque bloc. Cette surcharge est incluse dans le calcul de même que la surcharge due à l'eau (nappe phréatique au dessus du terrain) et que les forces dans les ancrages. Toutes ces forces sont projetées sur les directions horizontale et verticale, qui sont ensuite additionnées en composantes Fx_i et Fy_i.

K_h est une constante nommée coefficient d'accélération horizontale et est introduite dans le calcul afin de satisfaire l'équilibre sur des blocs individuels. Il existe une relation entre K_h et le facteur de stabilité de la pente SF permettant le calcul du coefficient de sécurité. Dans les cas ordinaires, le calcul se poursuit avec une valeur de K_h égale à zéro. Une valeur non nulle de K_h est utilisée pour simuler la surcharge horizontale, par exemple en raison d'un tremblement de terre (voir ci-dessous).

Processus de calcul

Calcul de l'équilibre limite

6n -1 inconnues sont nécessaires pour le calcul de l'équilibre limite, où n est le nombre de blocs divisant la région de sol au dessus de la surface de glissement potentielle. Elles sont :

5n -1 équations sont disponibles pour résoudre le problème, en particulier :

a) équations de force horizontale d'équilibre sur des blocs :

b) équations de force verticale d'équilibre sur des blocs :

c) équations de moment d'équilibre sur des blocs :

où rx_i et ry_i sont les bras de levier des forces Fx_i et Fy_i

d) Relation entre les forces normales et les forces de cisaillement selon la théorie de Mohr-Coulomb :

On peut voir que les n-1 inconnues doivent être estimées en premier. Une erreur relativement faible est admise lors de l'estimation des points d'application des forces E_i. Le problème devient alors déterminé statiquement. La résolution du système d'équations résultant fournit finalement les valeurs de toutes les inconnues restantes. Le principal résultat de cette analyse est la détermination du facteur d'accélération horizontale K_h.

Calcul du coefficient de stabilité de pente SF

Le coefficient de stabilité de la pente SF est introduit dans l'analyse de manière à réduire les paramètres de résistance du sol c et tgφ. Une analyse d'équilibre est ensuite effectuée pour que les paramètres réduits atteignent le coefficient d'accélération horizontale K_h pertinent pour un coefficient donné de stabilité de la pente SF. Cette itération est répétée jusqu'à ce que le facteur K_h atteigne zéro ou la valeur spécifiée.

Influence de charge extérieure

La pente analysée peut être chargée sur son sol par une charge inclinée ayant une forme généralement trapézoïdale. Cette charge entre dans le calcul de sorte que sa composante verticale (dans la direction du poids) est ajoutée au poids d'un bloc correspondant. Cela se traduit par une modification du poids de la tranche et de son centre de gravité. Si la composante verticale agit dans la direction opposée à celle de la gravité, elle est ajoutée à la force Fy_i. La composante horizontale est ajoutée à la force Fx_i.

Littérature :

Sarma, S. K.: Stability analysis of embankments and slopes,Géotechnique 23, 423-433, 1973.