Shahunyants
La méthode de Shahunyants est une méthode des tranches générale développée sur la base de l'équilibre limite. Elle nécessite un équilibre satisfaisant des forces et des moments agissant sur des blocs individuels. Les blocs sont créés en divisant le sol au-dessus de la surface de glissement par des plans de division. Les forces agissant sur les blocs individuels sont représentées sur la figure suivante.
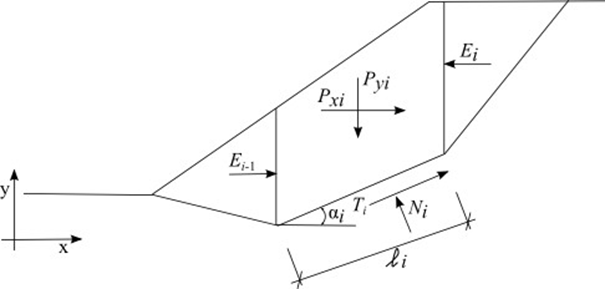Schéma statique - méthode de Shahunyants
Les forces suivantes sont supposées agir sur chaque bloc :
où : | Pyi | - | résultante des forces verticales agissant sur un bloc donné (poids du bloc, surcharge du bloc, séisme, forces d'ancrage…) |
Pxi | - | résultante des forces horizontales agissant sur un bloc donné (surcharge du bloc, séisme, forces d'ancrage, géo-renforcements…) | |
Ei+1, Ei | - | forces développées entre les blocs | |
Ni | - | réaction sous le bloc perpendiculaire au segment de surface de glissement | |
Ti | - | force de frottement agissant sur le segment de surface de glissement | |
αi | - | inclinaison du segment de surface de glissement | |
li | - | longueur du segment de surface de glissement | |
φi | - | angle de frottement interne du sol sur le segment de surface de glissement | |
ci | - | cohésion du sol sur le segment de surface de glissement |
Les hypothèses suivantes sont introduites dans la méthode de Shahunyants pour calculer l’état limite sur un bloc donné :
- les plans de division entre les blocs sont toujours verticaux
- l'inclinaison des forces Ei agissant entre les blocs est nulle, les forces agissent horizontalement
Méthode de résolution :
Dans un premier temps, les forces Pyi et Pxi sont transformées à l'aide des expressions (1) et (2) en PNi et PQi. Ainsi pour un angle positif αi (voir dessin ci-dessus) la force PNi (resp. PQi) agit dans la direction opposée à celle de Ni (resp. Ti). Les relations (1) et (2) décrivent une rotation d'angle αi.
(1)
(2)
Les forces agissant le long du segment de la surface de glissement sont définies par :
(3)
où : | Ui | - | pression interstitielle sur la surface de glissement |
Equations d'équilibre des forces satisfaites sur le bloc :
La condition d'équilibre dans la direction perpendiculaire au segment de la surface de glissement :
(4)
La condition d'équilibre dans la direction parallèle au segment de la surface de glissement :
(5)
Les équations (3) et (5) donnent trivialement :
(6)
De même, (4) et (6) donnent :
(7)
Après simplification, on obtient :
(8)
En utilisant la relation trigonométrique suivante:
(9)
l'équation (8) devient :
(10)
que l'on peut encore écrire :
(11)
et qui finalement fournit une relation de récurrence pour les forces Ei agissant entre les blocs :
(12)
Il est à présent temps d'introduire le coefficient de stabilité Ku. Le coefficient de stabilité est la valeur par laquelle les forces agissant sur les blocs de sol individuels sont amenées à un état d'équilibre. Ceci est obtenu en multipliant les forces actives (c’est-à-dire les forces contribuant au glissement de la masse du sol au-dessus de la surface de glissement) par le coefficient de stabilité. Dans l'équation (12), les forces actives sont contenues dans le terme PQi. Ce terme contient d'une part des forces actives qui contribuent au glissement et d'autre part des forces qui résistent au glissement, les forces contributives (resp. resistantes) sont notées PQi,sd (resp. PQi,ud). De là, la relation (12) devient :
(13)
Si la valeur de PQi est positive alors elle contribue au glissement et est donc considérée comme une force active PQi,sd. Si elle est négative alors elle s'oppose au glissement et est considérée une force résistante PQi,ud. Par conséquent en soustrayant la valeur PQi,ud, qui est négative, cela signifie dans l'équation (13) que l'on ajoute une valeur positive, on peut donc l'écrire formellement :
(14)
A l'origine de la surface de glissement, on a : E0 = 0. La valeur de E1 est alors donnée par :
(15)
La valeur de E2 par :
(16)
De même, on peut déterminer les valeurs de toutes les forces agissant entre les blocs. A l'autre extrémité de la surface de glissement, on a En = 0. En exploitant les relations précédentes, on obtient :
(17)
Cette expression fournit directement le coefficient de stabilité Ku par :
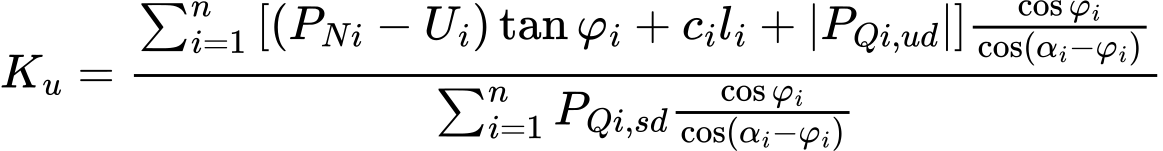(18)