Théorie de Sokolovski
D'après Sokolovski, la pression passive du sol est calculée en utilisant la formule suivante :
où : | Kpg | - | coefficient de butée des terres pour des sols non cohérents |
Kpc | - | coefficient de butée des terres en raison de la cohésion | |
Kpp | - | coefficient de butée des terres en raison de la surcharge du terrain | |
σz | - | contrainte verticale, totale |
Les relations pour déterminer l'intensité de la pression passive (butée) des terres et la surface de glissement sont décrites ici. La définition des variables est présentée dans la figure ci-dessous :
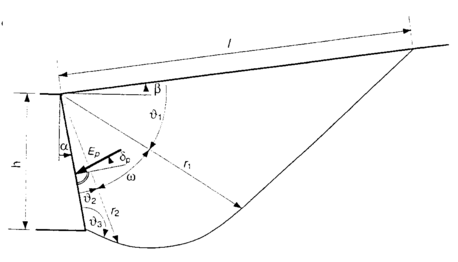Surface de glissement de la pression passive selon Sokolovski
Les angles qui déterminent la surface de glissement :
où : | φ | - | angle de frottement interne du sol |
δp | - | ||
β | - | inclinaison de la surface du terrain |
Rayon vecteur de la surface de glissement :
À condition que ω < 0, les deux bordures droites de la zone r1 et r2 se chevauchent et une surface plane est formée dans la zone de chevauchement. Les coefficients de butée Kpg ,Kpp et Kpc résultent des relations suivantes :
où : | φ | - | angle de frottement interne du sol |
δp | - | ||
α | - | inclinaison de la face arrière de la structure par rapport à la verticale |
variables auxiliaires : ipg, ipp, ipc, gpg, gpp, gpc, tpg, tpp, tpc
pour: |
| |
β ≤ 0 : |
| |
β > 0 : |
| |
α ≤ 0 : |
| |
α > 0 : |
|
, 
, 
, 
, 
, 
, 
où : |
|
Dans le cas où l'angle de frottement interne des sols est égal à zéro, les formules suivantes pour la butée s'appliquent :
où :
Littérature :
Sokolovski, V.V., 1ii960. Statics of Soil Media,Butterworth, London.