Материальные модели движения жидкости
Связь между скоростью движения жидкости и изменением гидравлической высоты (порового давления) подчиняется закону Дарси. В текущей версии программа предполагает постоянные значения коэффициентов фильтрации. Зависимость между коэффициентами проницаемости и поровым давлением не принимается во внимание.
Далее, задаётся начальный коэффициент пористости грунта e0,, позволяющий определить текущую пористость грунта n а затем фактическую скорость фильтрации жидкости, протекающей только по порам vs = v/n, где v - это средняя скорость фильтрации по всей площади просачивания. В общем случае справедливо, что коэффициенту пористости e0 = 1 соответствует пористость грунта n = 50 %.
В результате ввода коэффициента относительной проницаемости Kr программа позволяет отслеживать переход между полностью водонасыщенной средой (S = 1, Kr = 1) и ненасыщенной (Kr => 0) средой. Примером может послужить решение проблемы установившегося движения жидкости со свободным зеркалом. Переходом от полнонасыщенной среды в ненасыщенную можно управлять одной из трех моделей развития коэффициента относительной проницаемости Kr в зависимости от величины порового давления/статического напора, см. рис.
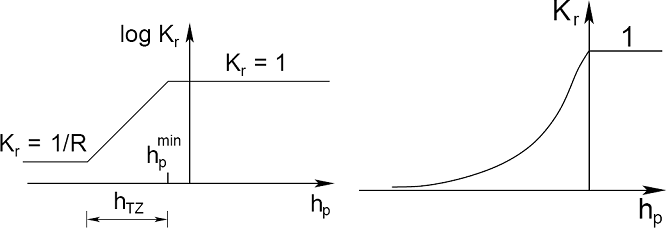 (а) Лог-линейная модель [1], (б) Модель Ван Генухтена [2]
(а) Лог-линейная модель [1], (б) Модель Ван Генухтена [2]
Лог-линейная модель
Лог-линейная модель переходной зоны описана, напр., в [1,3] и определена следующими параметрами:
hpmin | - | минимальное значение статического напора в полностью водонасыщенной среде [kPa] | |
hTZ | - | ширина переходной зоны [m] | |
R | - | параметр редукции, общее большое число R = от 100 до 1000 [-], настройка по умолчанию принята R = 1000 [-] |
Коэффициент относительной водопроницаемости Kr определяет выражение:
![]()
Модель Гарднера
Представляет собой эквивалентную модель, зависимую только от одного параметра α [1/m]. Коэффициент относительной водопроницаемости Kr в данном случае характеризован выражением [4]:
![]()
Модель Ван Генухтена
В этом случае величина коэффициента относительной водопроницаемости Kr определяется по формуле:
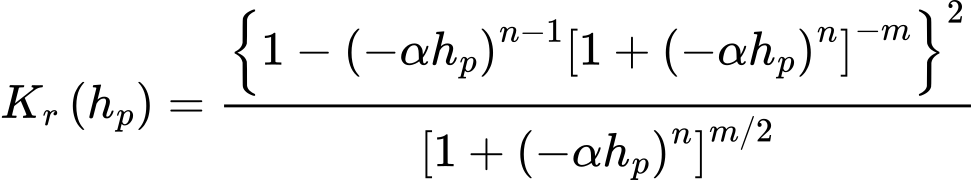
где α [1/m], n > 1, m = 1-1/n - это параметры модели, значения которых можно получить по лабораторным измерениям кривых водоудерживания апроксимированных отношением:
![]()
![]()
где: | Ssat | - | степень насыщения при полной сатурации, стандартная настройка Ssat = 1 |
Sr | - | остаточная степень насыщения | |
Θ | - | нормализованное содержание воды |
Параметр Θ в общем выражен как:
![]()
где: | θr | - | остаточное содержание воды [м3/м3] |
θS | - | содержание воды при полном насыщении грунта [м3/м3] |
Степень насыщения S может быть выражена как отношение содержания воды θ и пористости грунта n следующим образом (нужно различать n выражающее пористость и n в модели Ван Генухтена, это разные величины):
![]()
В Лог-линейной и Гарднера моделях использована упрощённая версия модели Ван Генухтена в соответствии с [5]:
![]()
где параметр b > 0 [-] вводим с целью более полно выразить водоудерживаюшие свойства данного грунта.
Рекомендуем следующую таблицу параметров, которые мы реально задаём. Это приведённые параметры к значениям, приводимым в исходных таблицах.
Ориентировочные значения параметров в модели ван Генухтена для разных способов классификации (сортировки) по величине зёрен USDA a FAO приведены в следующих таблицах.
Таблица с коэффициентами регрессии для 11 классов размера зерен МСХ США в соответствии с Ван Генухтена (1991)
Грунт (по величине зерна) | Ksat [м/день] | RETC | Rosetta | ||||||
e [-] | Sr [-] | α [1/м] | n 1[-] | e [-] | Sr [-] | α [1/м] | n [-] | ||
Песок | 7,13 | 0,75 | 0,11 | 14,5 | 2,68 | 0,60 | 0,14 | 3,5 | 3,18 |
Суглинистый песок | 3,50 | 0,70 | 0,14 | 12,4 | 2,28 | 0,64 | 0,13 | 3,5 | 1,747 |
Песчанистый суглинок | 1,06 | 0,70 | 0,16 | 7,5 | 1,89 | 0,63 | 0,10 | 2,7 | 1,448 |
Суглинок | 0,25 | 0,75 | 0,18 | 3,6 | 1,56 | 0,66 | 0,15 | 1,1 | 1,474 |
Мелкозернистый песок | 0,06 | 0,85 | 0,07 | 1,6 | 1,37 | 0,96 | 0,10 | 0,7 | 1,677 |
Иловый суглинок | 0,11 | 0,82 | 0,15 | 2,0 | 1,41 | 0,78 | 0,15 | 0,5 | 1,663 |
Песчаный жирный суглинок | 0,314 | 0,64 | 0,26 | 5,9 | 1,48 | 0,62 | 0,16 | 2,1 | 1,33 |
Жирный суглинок | 0,062 | 0,70 | 0,23 | 1,9 | 1,31 | 0,79 | 0,18 | 1,6 | 1,415 |
Илистые жирный суглинок | 0,017 | 0,75 | 0,21 | 1,0 | 1,23 | 0,93 | 0,19 | 0,8 | 1,52 |
Тощая глина | 0,029 | 0,61 | 0,26 | 2,7 | 1,23 | 0,63 | 0,30 | 3,3 | 1,207 |
Илистые глины | 0,0048 | 0,56 | 0,19 | 0,5 | 1,09 | 0,93 | 0,23 | 1,6 | 1,321 |
Глина | 0,048 | 0,61 | 0,18 | 0,8 | 1,09 | 0,85 | 0,21 | 1,5 | 1,253 |
Таблица с коэффициентами регрессии для 11 классов зернистости по ФАО в соответствии с Ван Генухтеном (1998)
Грунт (класс зернистости) | Ksat [м/сутки] | e [-] | Sr [-] | α [1/м] | n [-] |
Верхний слой грунта (до глубины 1 м) | |||||
Крупнозернистый (C) | 0,600 | 0,68 | 0,062 | 3,83 | 1,3774 |
Среднезернистый(M) | 0,121 | 0,78 | 0,023 | 3,14 | 1,1804 |
Средне-мелкозернистый (MF) | 0,023 | 0,75 | 0,023 | 0,83 | 1,2539 |
Мелкозернистый (F) | 0,248 | 1,08 | 0,019 | 3,67 | 1,0120 |
Тонкозернистый (VF) | 0,150 | 0,78 | 0,016 | 2,65 | 1,1033 |
Грунт в глубине (> 1 м) | |||||
Крупнозернистый (C) | 0,700 | 0,58 | 0,068 | 4,30 | 1,5206 |
Среднезернистый (M) | 0,108 | 0,65 | 0,026 | 2,49 | 1,1689 |
Средне-мелкозернистый (MF) | 0,040 | 0,70 | 0,024 | 0,82 | 1,2179 |
Мелкозернистый (F) | 0,085 | 0,93 | 0,021 | 1,98 | 1,0861 |
Тонкозернистый (VF) | 0,082 | 1,17 | 0,019 | 1,68 | 1,0730 |
Таблица: Система классификации текстуры грунтов по FAO
Грунт | Определение |
Крупнозернистый (C) Среднезернистый (M) | глина < 18% и песок > 65% 18%< глина < 35% и 15%< песок или: глина < 18% и 15%< песок < 65% |
Средне-мелкозернистый (MF) | глина < 35% и песок < 15% |
Мелкозернистый (F) | 35%< глина < 60% |
Тонкозернистый (VF) | 60%< глина |
Литература:
Подробная информация доступна в [2].
[1] D.M. Potts, L. Zdravkovič, Finite element analysis in geotechnical engineering - theory, Thomas Telford, London, 1999.
[2] M. Th. Van Genuchten, A closed formulation for predicting the hydraulic conductivity of unsaturated soils, Journal Soil Science Society of America 44, 239-259, 1988..
[3] M. Šejnoha, Finite element analysis in geotechnical design, to appear (2013)
[4] W. R. Gardner, Some steady-state solutions of the unsaturated moisture flow equation to evaporation from a water table, Soil Science 85(4), 228-232, 1958.
[5] M. Šejnoha, T. Janda, H. Pruška, M. Brouček, Modelování geotechnických úloh metodou konečných prvků: Teoretická základy a aplikace, předpokládaný rok vydání (2014)
[6] USDA 1951. Soil Survey Manual. Soil Conservation Service. U.S. Department of Agriculture Handbook No. 18. US Government Printing Office. Washington DC.
[7] Wösten, J.H.M., et. al. 1998. Using existing soil data to derive hydraulic parameters for simulation models in environmental studies and in land use planning. Final Report on the European Union Funded project. DLO Winand Staring Centre. Report 156, Wageningen, NL. p. 106. ISSN 0927-04537.