Полигональная поверхность скольжения
Решение задачи устойчивости откоса при использовании полигональной поверхности скольжения состоит в нахождении состояния предельного равновесия сил, действующих на массив грунта над поверхностью скольжения. Для того, чтобы можно было определить эти силы, грунт над поверхностью скольжения делим сечениями на блоки. Как правило, сечения выбирают вертикальными, но это не обязательное условие, напр., метод Сарма работает с наклонными плоскостями деления.
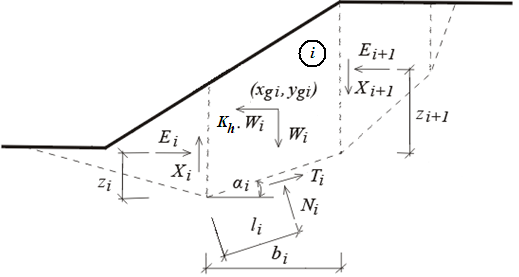 Статическая схема блока
Статическая схема блока
На рисунке показаны силы, действующие на отдельные блоки грунта. Если область над поверхностью скольжения разделена на n-ое количество блоков, то у нас будет следующих 6n-2 неизвестных: n значений нормальных сил Ni на участках поверхности скольжения, n значений относящихся к ним поперечных сил Ti; n-1 значений нормальных сил Ei между блоками грунта, n-1 значений поперечных сил Xi между блоками грунта; n-1 значений zi, определяющих точки приложения сил Ei, n значений li, обозначающие точки приложения Ni и одно значение степени устойчивости SF. Значения сил Xi могут быть в некоторых методах заменены значением наклона сил Ei.
Для решения задачи равновесия располагаем следующей системой уравнений: n горизонтальных и n вертикальных условий равновесия на блоках, n уравнений моментов равновесия на блоках и n отношений между силами Ni и Ti на блоках в соответствии с теорией Мора-Кулона. Следовательно, всего имеем 4n уравнения для 6n-2 неизвестных, из чего следует, что 2n-2 значений неизвестных необходимо выбрать предварительно. И как раз выбором этих значений и различаются отдельные методы решения.
Чаще всего, выбирают или местонахождения точек приложения отдельных сил или наклоны сил между блоками. Равновесие ищут с помощью итерации, когда предварительно подобранные значения должны удовлетворять условиям равновесия сил, а также обеспечивать кинематическую допустимости поученного решения.
Программа позволяет сделать расчёт с помощью следующих методов:
Можно оптимизировать поверхность скольжения и найти её наиболее критическое положение (самый низкий коэффициент устойчивости SF ).