Спенсер
Метод Спенсера - это общий метод отсеков предельного равновесия. Он требует удовлетворения условиям равновесия сил и моментов, действующих на отдельные блоки. Блоки создаются путем разделения области грунта над поверхностью скольжения плоскостями. Статическая схема блоков и действующих на них сил, показана на следующем рисунке.
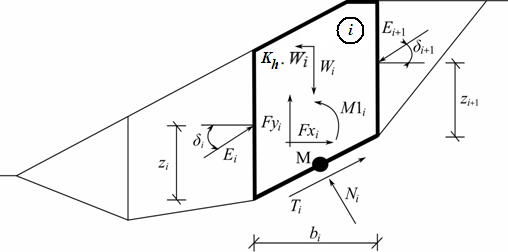Статическая схема: метод Спенсера
Предполагается, что каждый блок испытывает следующие усиления:
Wi | - | вес блока, включая напряжение материала, имеющего свойство блока, в т.ч. воздействие коэффициента вертикального землетрясения Kv |
Kh*Wi | - | горизонтальная инерционная сила, представляющая действие землетрясения, Kh - коэффициент горизонтального ускорения во время землетрясения |
Ni | - | нормальная сила на поверхности скольжения |
Ti | - | сила сдвига на поверхности скольжения |
Ei ,Ei+1 | - | силы, приложенные соседними блоками, они наклонены от горизонтальной поверхности на угол δ |
Fxi ,Fyi | - | другие горизонтальные и вертикальные силы, действующие на блок |
M1i | - | момент сил FxiFyi, вращающихся вокруг точки M, которая является центром i-ого сегмента поверхности скольжения |
Ui | - | равнодействующая порового давления на i-ом сегменте поверхности скольжения |
Для расчета предельного равновесия сил и моментов на отдельных блоках по методу Спенсера используются следующие допущения:
- плоскости раздела между блоками всегда вертикальны
- линия действия веса блока Wi проходит через центр i-ого сегмента поверхности скольжения, через точку M
- нормальная сила Ni действует в центре i-ого сегмента поверхности скольжения, в точке М
- наклонение сил Ei, действующих между блоками, является постоянной величиной для всех блоков и равно δ, только на крайних точках поверхности скольжения δ = 0
Решение принимает следующие выражения:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
где: | φi | - | угол внутреннего трения грунта на сегменте поверхности скольжения |
ci | - | удельное сцепление грунта на сегменте поверхности скольжения | |
αi | - | наклон сегмента поверхности скольжения |
Уравнение (1) представляет отношение между эффективным и полным значением нормальной силы на поверхности скольжения. Уравнение (2) - это уравнение Мора-Кулона, выражающее отношение между нор- уравнению момента равновесия вокруг точки M, где ygi - вертикальная координата точки приложения веса блока, а yM - вертикальная координата точки M. Изменяя уравнения (3) и (4), получаем следующую рекурсивную формулу:
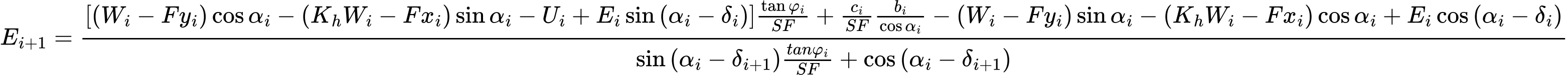
На основе этого отношения можно для δ и SF постепенно вычислить все силы Ei между блоками, исходя при этом из факта, что в начале поверхности скольжения значение Е известно: E1 = 0.
Из уравнения момента равновесия (5) выводится дополнительная рекурсивная формула:
Эта формула позволяет рассчитать для данных значений δ все плечи z сил, действующих между блоками, зная значение слева в начале поверхности скольжения, где z1 = 0.
Коэффициент надежности SF определяется при помощи следующего итерационного процесса:
- Начальное значение δ устанавливается равным 0, δ = 0.
- Коэффициент надежности SF для данного значения δ следует из уравнения (6), при этом допускается значение En+1 = 0 в конце поверхности скольжения.
- Значение δ рассчитывается уравнением (7) с помощью значений E, определенных на предыдущем этапе при условии, что момент на последнем блоке равен 0. Уравнение (7) не определяет значение zn+1, поскольку оно равно 0. Для этого значения должно выполняться уравнение момента равновесия (5).
- Этапы 2 и 3 повторяются до тех пор, пока значение δ не измениться.
Для обеспечения устойчивости процесса итерации необходимо избегать неустойчивых условий. Такие нестабильности появляются в точках, где имеет место деление на 0 в выражениях (6) и (7). В уравнении (7) деление на 0 принимается для δ = π/2 или δ = -π/2. Таким образом, значение угла δ должно находиться в интервале (-π/2;π/2).
Деление на 0 в выражении (6) имеет место, когда:
Еще одним способом предупредить цифровою нестабильность является проверка параметра mα: должно выполняться следующее условие:
Поэтому до начала итерации необходимо найти наивысшие показатели критических значений (SFmin), удовлетворяющих выше указанным условиям. Значения ниже данного критического значения SFmin находятся в области неустойчивого решения, поэтому итерация начинается с установки SF на значение «слегка» выше SFmin, и все итоговые значения SF выступающие в итерации больше, чем SFmin.
В общем можно сказать, что сложные методы труднее подвергаются конвергенции чем более простые методы (Bishop, Fellenius). Проблемы с конвергенцией возникают напр., на участках поверхности скольжения повышенной крутизны, сложной геометрии, при резком увеличении пригрузки и т.п. В случае, что расчёт не даёт результата, рекомендуется немного изменить задание, напр., уменьшить крутизну, в поверхность скольжения добавить больше точек и т.п. или выполнить расчёт по более простому методу.
Литература:
Spencer, E. 1967. A method of analysis of the stability of embankments assuming parallel interslice forces. Géotechnique, 17(1): 11-26.