0

FIN EC software

在线帮助

Tree
Settings
Program:
Language:

Bending resistance

The bending resistance is calculated for classes 1 and 2 using following formula

Where is:

Wpl,y, Wpl,z

  • The plastic section moduli for axes y and z

fy

  • The yield strength

γM0

  • The partial safety factor

The bending resistance for classes 3 and 4 is calculated in four points of the cross-section. These points are located in the corners of the cross-section. The following expression is used for the class 3

Where is:

iWy, iWz

  • The elastic section moduli of cross-section about the axes y and z in the i-point

fy

  • The yield strength

γM0

  • The partial safety factor

The following expression is used for the class 4

Where is:

iWeff,y, iWeff,z

  • The elastic section moduli of effective cross-section about the axes y and z in the i-point

fy

  • The yield strength

γM0

  • The partial safety factor

The bending resistance of perforated cross-section is calculated for classes 1 and 2 using following formula

Where is:

Wpl,y,osl,Wpl,z,osl

  • The plastic section moduli of perforated cross-section for axes y and z

fu

  • The yield strength

γM2

  • The partial safety factor

The following expression is used for the class 3

Where is:

iWy,osl, iWz,osl

  • The elastic section moduli of perforated cross-section about the axes y and z in the i-point

fu

  • The yield strength

γM2

  • The partial safety factor

The following expression is used for the class 4

Where is:

iWy,eff,osl, iWz,eff,osl

  • The elastic section moduli of effective perforated cross-section about the axes y and z in the i-point

fu

  • The yield strength

γM2

  • The partial safety factor

The minimum of the values Mc,Rd,y and Mc,Rd,y,osl or Mc,Rd,z and Mc,Rd,z,osl is used in the verification.

The design value of the resistance is reduced for "High shear" (described in the chapter "Low and high shear").

Where is:

iWpl,y,red, iWpl,z,red

  • The reduced plastic section moduli for axes y and z

fy

  • The yield strength

γM0

  • The partial safety factor

The reduced plastic section moduli are calculated as plastic section moduli with reduced capacity in walls that are subjected to "high shear". The reduction is based on the factors ρz and ρy that are calculated in accordance with the chapter "Low and high shear". The minimum of the values Mc,Rd,y and Mc,Rd,y,red or Mc,Rd,z and Mc,Rd,z,red is used in the verification.

Bending resistance including the effect of lateral torsional buckling

ÚThe bending resistance is given by the formula

Where is:

χLT,y, χLT,z

  • The reduction factors for lateral-torsional buckling

Mc,Rd,y, Mc,Rd,z

  • The bending resistances

The reduction factors for lateral-torsional buckling χLT,y and χLT,z depends on the value of the elastic critical moment for lateral-torsional buckling Mcr, that is calculated according to the expression

where the factor μcr is the critical moment given by following expressions

The non dimensional torsion factor kwt is calculated using formula

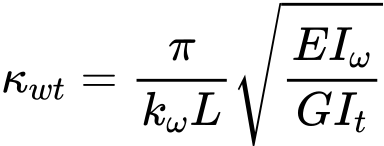
ζg is the non dimensional parameter considereing the load position relatively to the shear centre

ζj is the non dimensional parameter considereing the unsymmetry of cross-sections

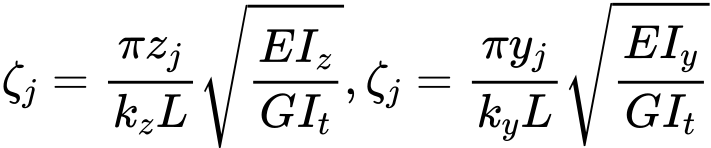
Where is:

C1, C2, C3

  • The parameters considering the load and end contions

kz, ky, kw

  • The buckling length factors

E

  • The modulus of elasticity

G

  • The shear modulus

Iz, Iy

  • The moments of inertia about axes y and z

L

  • The distance between two points where the lateral torsional buckling is prevented

Iω

  • The sectional moment of inertia

It

  • The rigidity moment in simple torsion

zg, yg

  • The horizontal and vertical distances of load position and shear centre

and zj and yj are given by expressions

Where is:

zs, ys

  • The horizontal and vertical distances of centre of gravity and shear centre

The relative slenderness is calculated with the help of the critical moment Mcr:

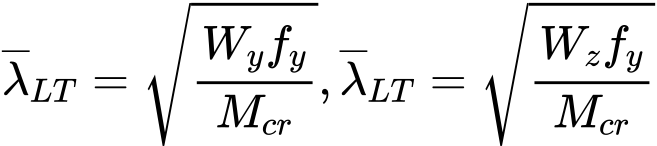
Where is:

Wy, Wz

  • The section moduli of cross-section about the axes y and z

The value of the imperfection factor αLT is set according to the buckling curves a, b, c, d. The factors χLT,y and χLT,z are given by expressions

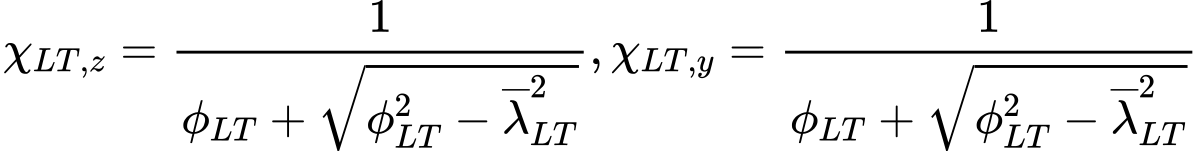
however, following condition has to be fulfilled

where

The effect of lateral torsional buckling isn't considered for cross-sections resistant to LT buckling (e.g. RHS) and for cases, where the bending moment acts about the weak axis of the cross-section.

Try FIN EC software yourself. Download Free Demoversion.

更多免费培训资料

试用版

免费试用软件

视频教程

观看有关如何在实践中使用我们软件的简短视频。

工程手册

这些手册将引导您一步一步完成特定的设计任务。