Verification of buckling resistance of built-up cross-sections
The buckling resistance perpendicular to the strong axis is given by expression
Where is: | χ |
|
A |
| |
fy |
| |
γM1 |
|
The effective cross-sectional area is considered for class 4.
The slenderness λy in the direction perpendicular to the strong axis y is given by formula
Where is: | Lcr,y |
|
iy |
|
The relative slenderness 
is given by the expression
Where is: | λy |
|
λ1 |
| |
Aeff |
| |
A |
|
The slenderness value λ1 is given by the formula
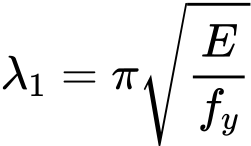
Where is: | E |
|
fy |
|
The value of the imperfection factor α is set according to the buckling curves a, b, c, d. The factor χy corresponds to the relative slenderness 
and is calculated using expression
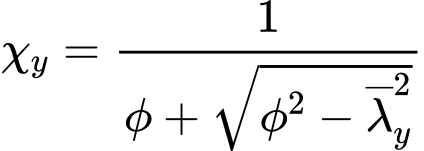
however, following condition has to be fulfilled
where
The partial cross-section fails if the specified axial force is greater than the resistance Nb,Rd,y.
The calculation of buckling resistance perpendicular to the weak axis follows. The elastic flexural buckling force Ncr is given by the expression
Where is: | lcr,z |
|
kE,θ |
| |
E |
| |
Ieff |
|
Following formula is used for Ieff for lacing
Where is: | h0 |
|
A |
|
The second moment of area I1 is calculated for built-up cross-sections with battens using the expression
Where is: | A |
|
h0 |
| |
Iz |
|
The radius of gyration i0 is given by the expression
For the slenderness
the factor μ is selected. The effective value of the moment of inertia Ieff is given by the expression
The partial cross-section fails if the specified axial force is greater than the resistance Ncr.
The verification of the shear stiffness SV follows. The shear stiffness is given by the follwoing formula for battens
or
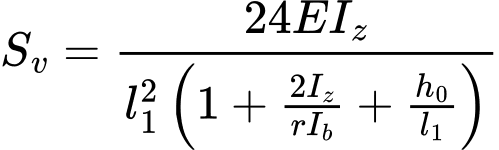
However, following expression has to be fulfilled
Where is: | l1 |
|
r |
| |
Ib |
| |
h0 |
|
The axial force shouldn't exceed the shear stiffness SV. Also following expression has to be fulfilled
The force in the middle of the batten is calculated using formula
The force in lacing is
Where the moment MS is given by the expression
Where is: | e0 |
|
The buckling resistance is given by expression
Where is: | χy |
|
A |
| |
fy |
| |
γM1 |
|
where the factor χz corresponds to the slenderness λ, that is given by the expression
Where is: | l1 |
|
imin |
|
The relative slenderness 
is given by the formula
where
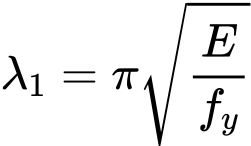
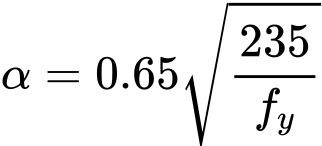
The value of the imperfection factor α is set according to the buckling curves a, b, c, d. The factor χz corresponds to the relative slenderness 
and is calculated using expression
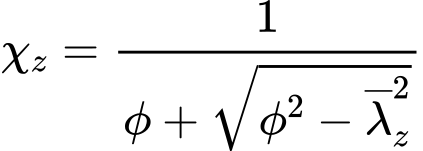
however, following condition has to be fulfilled
where
where
The shear force VS is calculated for the batten
Where the moment MS is given by the expression
Where is: | l1 |
|
Vy |
|
The bending resistance of partial cross-section for bending moment My is calculated for the classes 1 and 2 according to the following formula:
The formula for the class 3:
The formula for the class 4:
Where is: | Wpl,y |
|
Wy |
| |
Wy,eff |
|
The bending resistance of partial cross-section for bending moment Mz is calculated for the classes 1 and 2 according to the following formula:
The formula for the class 3:
The formula for the class 4:
Where is: | Wpl,z |
|
Wz |
| |
Wz,eff |
|
The verification is done for two points: the mid point of the distance between two battens and in the connection of batten.
The verification in the mid point of the distance between two battens:
Where is: | n |
|
dN |
| |
ky |
|
The verification in the connection of batten:
