在线帮助

Primary Settlement

The final primary settlement s is often substituted by the term settlement. Most of the computational approaches can be attached to one of the two groups:

• Linear elastic deformation
• Nonlinear elastic deformation

Linear elastic deformation

The linear stress-strain relationship follows the Hook law:

The applicability of Young's modulus E of elasticity is substantiated only in cases, in which the stressed soil is allowed to stretch in the horizontal direction. This, however, is acceptable only for small spread foundations. When applying the load over a larger area, the stressed soil cannot, except for its edges, to deform sideways and experiences therefore only a vertical (one-dimensional) strain related to the oedometric modulus E_oed, that is larger than the elastic modulus E.

The settlement of a soil layer s is determined by multiplying the deformation of a soil layer ε by the layer thickness (height) H_o:

In case of layered subsoil we get the total settlement by summing up settlements of individual layers:

Nonlinear elastic deformation

For most soils the stress-strain relationship is nonlinear and often influenced by the load history. This nonlinearity cannot be neglected, particularly when computing the settlement of fine-grained soils (silts, clays). Clearly, the procedure based on the application of Young's modulus of elasticity is not generally applicable. Even if employing the stress-dependent oedometric modulus of deformation, it will not be possible to receive reasonable estimates of the behavior of certain overconsolidated soils. Nonlinear elastic deformation is generally modeled using the void ratio and deformation characteristics derived from one-dimensional deformation of a soil sample (e.g. compression constant, compression index, etc.).

The procedure for the computation of settlement of a compressible saturated soil layer using the void e is described on the following soil element having the height H_o and the width B = 1 m:

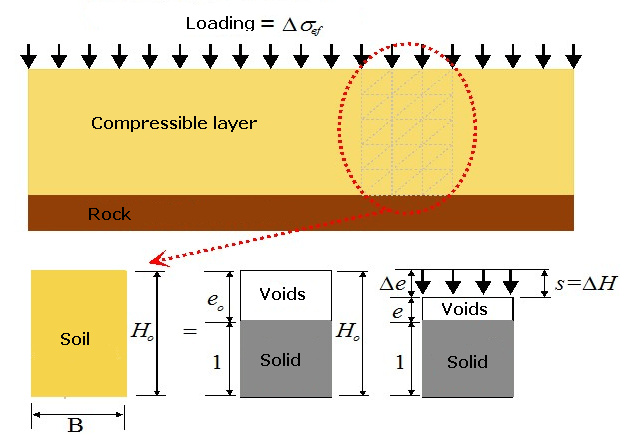Analysis of settlement from the phase diagram

Because the soil is a three-phase medium (it contains solid particles and pore filled with fluid and gas) it is possible to describe the solid particles (rock particles and mineral grains) by their volume V_s (and assumed to be equal to unity), while the porous phase can be described using the void ratio e.

The soil element is subjected on its upper surface to a uniform load q causing the change in stress inside the sample and also the vertical displacement ΔH, which in turn leads to the reduction of pores V_p and therefore also to the reduction of void ratio (from its original value e_o to a new value e). The vertical strain ε of a soil sample is given by the ratio of ΔH to the original sample height H_o, and can be expressed using the void ratio e:

By modifying this equation we arrive at the formula describing the sample settlement with the help of void ratio: