Spencer
La méthode de Spencer est une méthode des tranches générale développée sur la base de l'équilibre limite. Elle nécessite un équilibre satisfaisant des forces et des moments agissant sur des blocs individuels. Les blocs sont créés en divisant le sol au-dessus de la surface de glissement par des plans de division. Les forces agissant sur les blocs individuels sont représentées sur la figure suivante.
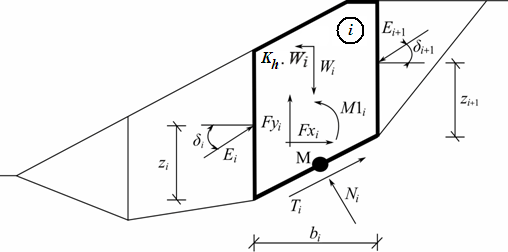 Schéma statique - méthode de Spencer
Schéma statique - méthode de Spencer
Les forces suivantes sont supposées agir sur chaque bloc :
Wi | - | poids du bloc, y compris la charge de gravité et l'effet du coefficient de séisme vertical Kv |
Kh*Wi | - | force d'inertie horizontale représentant l'effet du séisme, Kh coefficient d'accélération horizontale |
Ni | - | force normale sur la surface de glissement |
Ti | - | force de cisaillement sur la surface de glissement |
Ei, Ei+1 | - | forces exercées par les blocs voisins, ils sont inclinés par rapport au plan horizontal d'un angle δi |
Fxi,Fyi | - | autres forces horizontales et verticales agissant sur le bloc |
M1i | - | moment des forces Fxi, Fyi tournant autour du point M, qui est le milieu du ième segment de la surface de glissement |
Ui | - | pression interstitielle résultante sur le ième segment de la surface de glissement |
Les hypothèses suivantes sont introduites dans la méthode de Spencer pour calculer l’équilibre limite des forces et des moments sur des blocs individuels :
- les plans de divisions entre les blocs sont toujours verticaux
- la ligne d'action du poids du bloc Wi passe par le milieu du ième segment de la surface de glissement représenté par le point M
- la force normale Ni agit au milieu du ième segment de la surface de glissement représenté, au point M
- l'inclinaison des forces Ei agissant entre les blocs est constante pour tous les blocs et égale à δi, par contre aux points d'extrémité de la surface de glissement δi est nulle
La solution prend alors la forme suivante :
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
où : | φi | - | angle de frottement interne du sol sur la surface de glissement |
ci | - | cohésion du sol sur la surface de glissement | |
αi | - | inclinaison du segment de surface de glissement |
L'équation (1) représente la relation entre la valeur effective et la valeur totale de la force normale agissant sur la surface de glissement. L'équation (2) correspond à la condition de Mohr-Coulomb représentant la relation entre les forces normales et les forces de cisaillement sur une portion donnée de la surface de glissement. L'équation (3) représente l'équation d'équilibre des forces dans la direction normale au ième segment de la surface de glissement, tandis que l'équation (4) représente l'équation d'équilibre le long du segment de la surface de glissement. SF est le coefficient de sécurité utilisé pour réduire les coefficients du sol. L'équation (5) correspond à l'équation d'équilibre des moments autour du point M, où ygi est la coordonnée verticale du point d'application du poids du bloc et yM la coordonnée verticale du point M. La modification des équations (3) et (4) fournit la relation de récurrence suivante :
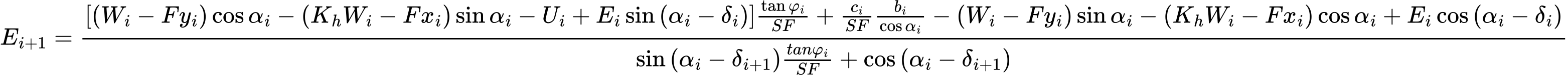
Cette formule permet de calculer toutes les forces Ei agissant entre les blocs pour des valeurs données de δi et SF. Cette solution suppose qu'à l'origine de la surface de glissement, la valeur de E soit connue et vérifie E1 = 0.
La relation de récurrence supplémentaire (découlant de l'équation d'équilibre des moments (5)) donne :
![]()
Cette formule permet de calculer pour une valeur donnée de δ tous les bras de levier z agissant entre les blocs. La valeur à gauche de l’origine de la surface de glissement est z1 = 0.
Le coefficient de sécurité SF est déterminé en utilisant le processus itératif suivant :
- La valeur initiale de l'angle δ est nulle : δ = 0.
- Le coefficient de sécurité SF, pour une valeur donnée de δ, découle de l'équation (6), en supposant la valeur En+1 = 0 à la fin de la surface de glissement.
- La valeur de δ est fournie par l'équation (7) en utilisant les valeurs de E déterminées à l'étape précédente avec la nécessité d'avoir le moment nul sur le dernier bloc. L'équation (7) ne fournit pas la valeur de zn+1 car elle est nulle. Pour cette valeur, l'équation d'équilibre des moments (5) doit être satisfaite.
- Les étapes 2 et 3 sont ensuite répétées jusqu'à ce que la valeur de δ ne change plus.
Pour que le processus itératif reste stable, il est nécessaire de supprimer les cas de divergences. Elles apparaissent lors de division par zéro dans les équations (6) et (7). Dans l'équation (7), la division par zéro apparait pour δ = π/2 ou δ = -π/2. Ainsi la valeur de δ doit se trouver dans l'intervalle ]-π/2,π/2[.
La division par zéro apparait dans l'équation (6) quand :
![]()
La valeur du paramètre mα est une autre source d'instabilité numérique, pour l'éviter, la condition suivante doit être satisfaite :
![]()
Par conséquent, avant de lancer les itérations, il est nécessaire de trouver la plus grande des valeurs critiques SFmin satisfaisant aux conditions mentionnées ci-dessus. Les valeurs inférieures à cette valeur critique SFmin se trouvent dans la zone d'instabilité des solutions. Par conséquent, les itérations commencent en définissant SF sur une valeur «juste» au-dessus de SFmin et toutes les valeurs de FS obtenues par les calculs itératifs sont supérieures à FSmin.
Généralement les méthodes rigoureuses convergent moins bien que les méthodes plus simples (Bishop, Fellenius). Des exemples de problèmes de convergence proviennent de sections trop pentues de la surface de glissement, d'une géométrie complexe, d'un saut de surcharge significatif, etc. Si aucun résultat n'est obtenu, nous recommandons de modifier légèrement les données d'entrée (par exemple une surface de glissement moins pentue, introduire plus de points sur la surface de glissement, etc.) ou d'utiliser des méthodes plus simples.
Littérature :
Spencer, E. 1967. A method of analysis of the stability of embankments assuming parallel interslice forces. Géotechnique, 17(1): 11-26.