Options d'analyse des contraintes

Le programme GEO5 MEF réalise l'analyse contrainte-déformation en tenant compte des conditions soit drainées, soit non drainées. Cette option est à fixer lors de la définition du modèle de matériau. L'application des conditions drainées est l'option par défaut. Cette option considère un état stationnaire des pressions interstitielles (p = p^ss), c'est-à-dire l'état atteint à la fin de la consolidation au temps . L'effet de succion n'est pas pris en compte. Cela signifie qu'au-dessus de la nappe phréatique, le degré de saturation est S = 0, tandis qu'en dessous de la nappe phréatique, on fixe S = 1. L'analyse est effectuée en utilisant les contraintes effectives ainsi que les paramètres de résistance au cisaillement effectifs. La pression interstitielle est introduite dans l'analyse sous forme de chargement imposé. En revanche, les conditions non drainées supposent que l'analyse est réalisée au début de la consolidation, au temps t = 0. Par exemple, on peut considérer le cas d'une excavation dans un sol saturé à faible perméabilité. Ce type d'analyse génère des pressions interstitielles en excès (p = p^ex​). Le programme GEO5 MEF propose trois options pour la prise en compte des conditions non drainées :

Analyse en contraintes effectives (c_ef, φ_ef)

Cette option (Type 1) est disponible pour tous les modèles de matériau. L'analyse est réalisée en contraintes effectives tout en tenant compte des paramètres de résistance au cisaillement effectifs. Les paramètres de base décrivant le comportement élastique du matériau, à savoir le module d'élasticité et le coefficient de Poisson, correspondent aux conditions drainées. Sur l’hypothèse d’une incompressibilité volumique, l’analyse introduit une matrice de raideur effective. Lorsque la solution prend en compte l’introduction ou la variation de la nappe phréatique, la pression interstitielle résultante est la somme de la pression interstitielle stabilisée et de la pression interstitielle en excès, soit p = p^ss + p^ex​. Dans les modèles de matériau qui considèrent la dilatance à l’aide de l’angle de dilatance ψ (ainsi que l’angle de dilatance mobilisé ψ_m​ dans le modèle Hardening Soil), la valeur de ψ est fixée à zéro.

Contrairement au comportement réel des sols, cette approche suppose que la contrainte effective ne varie pas. Cela peut conduire à une surestimation significative de la contrainte déviatorique à la rupture. La résistance au cisaillement mobilisée dépasse ainsi la résistance au cisaillement non drainé du sol considéré, comme le montre la figure ci-dessous. Le programme permet la visualisation de la résistance au cisaillement non drainé prévue numériquement , où J est la contrainte déviatorique équivalente et θ est l’angle de Lode. Cette valeur devrait être inférieure à la véritable résistance au cisaillement non drainé . Il est recommandé à l’utilisateur de vérifier cette condition, en particulier lorsqu’il adopte des modèles de matériau élastiques parfaitement plastiques.

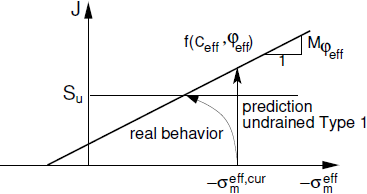
Analyse en contraintes effectives (S_u)

Cette option (Type 2) est disponible uniquement pour les modèles de type Mohr-Coulomb (Drucker-Prager, Mohr-Coulomb, Mohr-Coulomb modifié). L’analyse est réalisée de manière analogue à l’option précédente, en incluant la formulation de la matrice de raideur effective et la détermination de la pression interstitielle en excès. La pression interstitielle résultante est la somme de la pression interstitielle stabilisée et de la pression interstitielle en excès, soit p = p^ss + p^ex. L’angle de dilatance ψ est de nouveau fixé à zéro. La seule différence, mais essentielle, réside dans l’application des paramètres de résistance au cisaillement en contraintes totales. Le coefficient de cohésion effectif c est remplacé par la résistance au cisaillement non drainé S_u(c_u), et l’angle de frottement interne φ est supposé nul (φ_u = 0).

Du point de vue numérique, la fonction de charge de Drucker-Prager est remplacée par la fonction de charge de von Mises. De même, la fonction d'écoulement plastique de Mohr-Coulomb est remplacée par celle de Tresca. D’un point de vue pratique, cette option permet de prendre en compte la valeur réelle de S_u​, car elle est directement utilisée comme paramètre d’entrée. Néanmoins, les pressions interstitielles prévues, et par conséquent les contraintes effectives, pourraient ne pas être complètement correctes.

Analyse en contraintes totales (S_u)

Cette option (Type 3) est disponible uniquement pour les modèles de type Mohr-Coulomb (Drucker-Prager, Mohr-Coulomb, Mohr-Coulomb modifié). L’analyse est réalisée en contraintes totales. Les paramètres de raideur (module d'élasticité et coefficient de Poisson ) ainsi que les paramètres de résistance au cisaillement sont considérés comme des valeurs totales. Si la procédure K₀​ est adoptée, il est prévu que les contraintes générées correspondent aux contraintes totales.

La variation potentielle de la pression interstitielle stabilisée dans le sol situé sous la nappe phréatique n’est pas prise en compte dans l’analyse. De même, aucune variation de la pression interstitielle en excès n’est générée, et la pression interstitielle totale courante est fixée à zéro, soit p = 0. Par conséquent, la variation des contraintes effectives correspond directement à la variation des contraintes totales. Cela se reflète également dans la représentation graphique de ces variables. Ainsi, toute variation potentielle de la pression interstitielle ne peut pas être visualisée. L’utilisateur doit en être conscient.