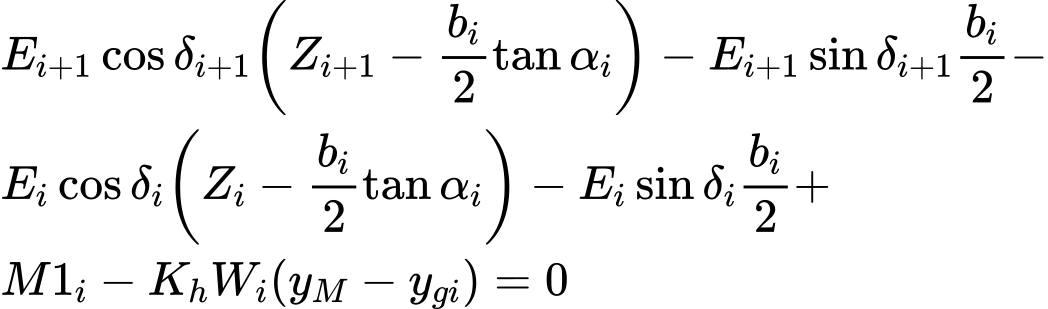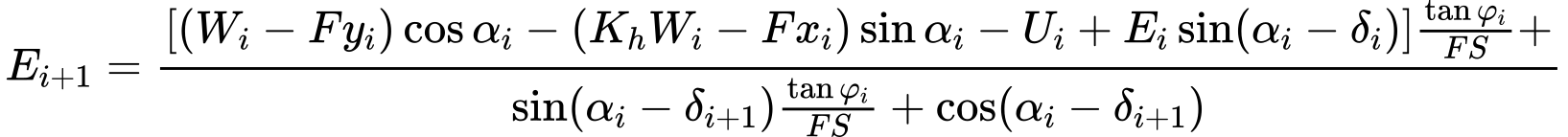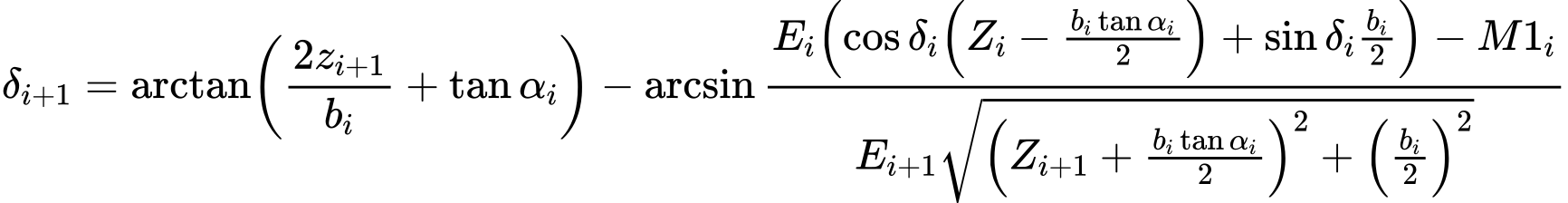Janbu
O método de Janbu baseia-se na análise do estado de equilíbrio limite. Este método implica que o equilíbrio de forças e momentos seja verificada para cada bloco (excluindo o bloco superior, onde o equilíbrio de momentos não é verificado). Os blocos consistem na divisão do perfil do talude através de planos divisores. As forças atuam em cada bloco de acordo com a seguinte figura:
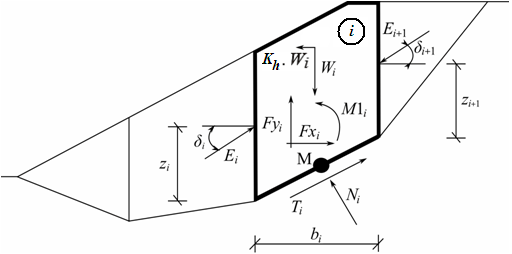 Esquema das forças atuantes - Método de Janbu
Esquema das forças atuantes - Método de Janbu
Cada bloco estará sujeito às forças seguintes:
Wi | - | peso do bloco, incluindo o valor da componente material vertical de sobrecargas com direção descendente, considerando a influência do coeficiente sísmico vertical Kv |
Kh*Wi | - | momento de inércia horizontal considerando o efeito sísmico, onde Kh é o coeficiente sísmico horizontal |
Ni | - | força normal atuante na superfície do talude |
Ti | - | força de cisalhamento atuante na superfície do talude |
Ei ,Ei+1 | - | forças exercidas por blocos vizinhos, com um ângulo de inclinação δi e δi+1, respetivamente, medido a partir do plano horizontal e à cota zi e zi+1, respetivamente, acima da superfície de deslizamento |
Fxi,Fyi | - | outras forças horizontais e verticais atuantes no bloco |
M1i | - | momentos das forças Fxi, Fyi em relação ao ponto M, que representa o centro do iésimo segmento da superfície de deslizamento |
Ui | - | empuxo resultante no iésimo segmento da superfície de deslizamento |
Para calcular o equilíbrio de forças e momentos limite através do método de Janbu, são consideradas as seguintes premissas:
- os planos que divisores dos blocos são sempre verticais
- a linha de ação do peso do bloco Wi atravessa o centro do iésimo segmento da superfície de deslizamento, representado pelo ponto M
- a força normal Ni atua no centro do iésimo segmento da superfície de deslizamento, representado pelo ponto M
- a posição zi das forças Ei atuantes entre blocos é para os limites da superfície de deslizamento é assumida como z = 0
A escolha da posição zi pode influenciar significativamente a convergência do método. Caso seja adotada uma má posição zi para um dado talude, poderá ser impossível verificar as condições de equilíbrio (algoritmo não convergente). As alturas zi acima da superfície de deslizamento são definidas para aproximadamente um terço da altura da interface entre blocos. No caso das condições de equilíbrio não serem satisfeitas, o algoritmo altera as alturas, ex.: ligeiramente acima, dentro da zona passiva, próximo da base do talude; ligeiramente abaixo, dentro da zona ativa, próximo do topo do talude.
A solução assenta nas seguintes equações:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
onde: | φi | - | ângulo de atrito interno do solo no segmento da superfície de deslizamento |
ci | - | coesão do solo no segmento da superfície de deslizamento | |
αi | - | inclinação do segmento da superfície de deslizamento |
A Equação (1) representa a relação entre os valores efetivo e total da força normal atuante na superfície de deslizamento. A Equação (2) corresponde à condição de Mohr-Coulomb que representa a relação entre as forças normal e de cisalhamento para um dado segmento da superfície de deslizamento. A Equação (3) representa a equação de equilíbrio de forças com direção normal ao iésimo segmento da superfície de deslizamento, enquanto que a Equação (4) representa o equilíbrio no iésimo segmento da superfície de deslizamento. FS é o fator de segurança, que é utilizado para reduzir os valores das características do solo. A Equação (5) corresponde à equação de equilíbrio de momentos em relação ao ponto M, onde ygi é a coordenada vertical do ponte de aplicação do peso do bloco e yM é a coordenada vertical do ponto M.
A partir das Equações (3) e (4) obtém-se a seguinte equação:
| (6) |
Esta fórmula permite calcular todas as forças Ei que atuam entre blocos, para os valores de δi e FS considerados. Esta solução assume que o valor de E para a origem da superfície de deslizamento é conhecido e igual a E1 = 0.
A partir da Equação (5) de equilíbrio de momentos obtém-se a seguinte Equação (7), para calcular os ângulos δi:
| (7) |
Esta equação permite calcular, para um dado valor de δ, todos os braços zi das forças atuantes entre blocos, conhecendo o valor à esquerda da origem da superfície de deslizamento, onde z1 = 0.
O fator de segurança FS é determinado através do seguinte processo iterativo:
- O valor inicial para os ângulos é definido como zero δi = 0 e as posições zi como aproximadamente um terço da altura da interface.
- O fator de segurança FS para um dado valor de δi é obtido através da Equação (6), assumindo o valor de En+1 = 0 para o limite da superfície de deslizamento.
- O valor de δi é obtido através da Equação (7), considerando os valores de Ei determinados no passo anterior.
- O passos 2 e 3 são repetidos até que o valor de FS não se altere.
É necessário evitar soluções instáveis para que o processo iterativo seja bem sucedido. As instabilidade podem ocorrer quando existem divisões por zero na Equação (6):
![]()
Outra verificação que deve ser verificada para prevenir a instabilidade numérica é a do parâmetro mα - a seguinte condição deve ser verificada:
![]()
Assim, antes de iniciar o processo iterativo, é necessário obter o valor mais crítico FSmin que satisfaça todas as condições referidas. Os valores inferiores a este valor crítico FSmin representam soluções instáveis, sendo que o processo iterativo terá início com a definição de FS como um valor imediatamente acima de FSmin e, consequentemente, todos os valores de FS do processo iterativo serão superiores a FSmin.
Geralmente, a convergência de métodos rigorosos é pior que a de métodos mais simples (Bishop, Fellenius). Como exemplos, os problemas de convergência podem ser encontrados para secções demasiado inclinadas de superfícies de deslizamento, geometrias complexas, variações de sobrecargas elevadas, etc. Caso não seja obtido nenhum resultado, é recomendável uma ligeira alteração nos dados introduzidos, ex.: inclinação da superfície de deslizamento menos acentuada, introduzir mais pontos na superfície de deslizamento, etc, ou recorrer a métodos mais simples.
Bibliografia:
Janbu, N. 1954. Application of Composite Slip Surface for Stability Analysis. European Conference on Stability Analysis, Stockholm, Sweden.
Janbu, N. 1973. Slope Stability Computations. Embankment Dam Engineering - Casagrande Volume, R.C. Hirschfeld and S.J. Poulos, eds., John Wiley and Sons, New York, pp 47-86.